A box contains 3 white balls, 4 black balls and 5 yellow balls. In how many ways can 4 balls be drawn from the box, if at least one yellow ball is to be included in the draw?
We may have (1 yellow and 3 others) or (2 yellow and 2 others) or (3 yellow and 1 others) or (4 yellow).
Therefore, Required number of ways= (4C1*8C3)+ (4C2*8C2)+ (4C3*8C1)+ (4C4)
= 4* 8*7*6 + 4*3 * 8*7 + (4C1*8) +1
3*2*1 2*1 2*1
= 224+168+32+1= 425
There are 6 red shoes & 4 green shoes . If two of red shoes are drawn what is the probability of getting red shoes
Total no.of shoes=6+4=10;
from total two shoes drawn=10c2
two of red shoes are drawn=6c2
so from 10 shoes propability of drawing two red shoes=6c2/10c2
6 parallerl lines are intersected by 5 other parallel lines. The total number of parallelogram formed is
Any two lines in one direction and any two parallel lines in the other direction can form a parallograms.
So, number of parallogram formed
= 6c2 x 5c2 = 6!/(4!*2!) +5!/(3!*2!) =150
In how many ways can 21 books on English and 19 books on Hindi be placed in a row on a shelf so that two books on Hindi may not be together?
In order that two books on Hindi are never together, we must place all these books as under:
X E X E X E X …. X E X
Where E – denotes the position of an English book and X that of a Hindi book.
Since there are 21 books on English, the number of places marked X are therefore, 22. Now, 19 places out of 22 can be chosen in
22C19 = 22C3 = (22 x 21 x 20)/3 x 2 x 1 = 1540 ways
Hence, the required number of ways = 1540.
How many words can be formed by re-arranging the letters of the word ASCENT such that A and T occupy the first and last position respectively?
As A and T should occupy the first and last position, the first and last position can be filled in only one way. The remaining 4 positions can be filled in 4! Ways by the remaining words (S,C,E,N,T). hence by rearranging the letters of the word ASCENT we can form 1×4! = 4! words.
Find the number of ways in which one or more letter be selected from the letters AAAABBCCCDEF.
The number of ways of
Selecting A = 4+1 = 5
Selecting B = 2+1 = 3
Selecting C = 3+1 = 4
Selecting D = 1+1 = 2
Selecting E = 1+1 = 2
Selecting F = 1+1 = 2
Hence, total ways of selecting = 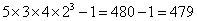
How many permutations of 3 different digits are there, chosen from the ten digits 0 to 9 inclusive?
The number of permutations of 3 digits chosen from 10 is 10P3 = 10 × 9 × 8 = 720
It is required to seat 7 men and 3 women in a row such that women should occupy even places how many such arrangements are possible ?
All the 10 persons should be arranged in a row
And in a row of 10 positions there are exactly 5 even places.
3 of these even places should be occupied by 3 women
this can be done in 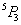 Ways.
Ways.
The remaining 7 positions can be filled by the 7 men in 7 p 7Ways
Hence, the total number of seating arrangements
= 5P 3 x 7 P 7
= 302400
How many different four letter words can be formed (the words need not be meaningful) using the letters of the word “MEDITERRANEAN” such that the first letter is E and the last letter is R?
The first letter is E and the last one is R.
Therefore, one has to find two more letters from the remaining 11 letters.
Of the 11 letters, there are 2 Ns, 2Es and 2As and one each of the remaining 5 letters.
The second and third positions can either have two different letters or have both the letters to be the same.
Case 1: When the two letters are different. One has to choose two different letters from the 8 available different choices. This can be done in 8 * 7 = 56 ways.
Case 2: When the two letters are same. There are 3 options – the three can be either Ns or Es or As. Therefore, 3 ways.
Total number of posssibilities = 56 + 3 = 59.
Tickets numbered 1 to 20 are mixed up and then a ticket is drawn at random. What is the probability that the ticket drawn has a number which is a multiple of 3 or 5?
Here, S = {1, 2, 3, 4, …., 19, 20}.
Let E = event of getting a multiple of 3 or 5 = {3, 6 , 9, 12, 15, 18, 5, 10, 20}.
P(E)= n(E)/n(S)= 9/20