| 27. | A train overtakes two persons who are walking in the same direction in which the train is going, at the rate of 2 kmph and 4 kmph and passes them completely in 9 and 10 seconds respectively. The length of the train is: | ||||||||||||||||||||||||||||||||||||||||||||
Answer: Option B Explanation:
Let the length of the train be x metres and its speed by y m/sec.
On solving, we get: x = 50.
|
| 28. | A train overtakes two persons walking along a railway track. The first one walks at 4.5 km/hr. The other one walks at 5.4 km/hr. The train needs 8.4 and 8.5 seconds respectively to overtake them. What is the speed of the train if both the persons are walking in the same direction as the train? | ||||||||||||||||||||||||||||||||||
Answer: Option D Explanation:
Let the speed of the train be x m/sec. Then, (x – 1.25) x 8.4 = (x – 1.5) x 8.5
|
| 29. | A train travelling at 48 kmph completely crosses another train having half its length and travelling in opposite direction at 42 kmph, in 12 seconds. It also passes a railway platform in 45 seconds. The length of the platform is | |||||||||||||||||||||||||||||||||||||||||
Answer: Option A Explanation:
Let the length of the first train be x metres.
Let the length of platform be y metres.
|
| 30. | Two stations A and B are 110 km apart on a straight line. One train starts from A at 7 a.m. and travels towards B at 20 kmph. Another train starts from B at 8 a.m. and travels towards A at a speed of 25 kmph. At what time will they meet? | |||||||
Answer: Option B Explanation:
Suppose they meet x hours after 7 a.m. Distance covered by A in x hours = 20x km. Distance covered by B in (x – 1) hours = 25(x – 1) km.
So, they meet at 10 a.m. |


 Length of faster train =
Length of faster train =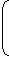

 9y – x = 5 and 90y – 9x = 100.
9y – x = 5 and 90y – 9x = 100.