| 2. | If log 2 = 0.3010 and log 3 = 0.4771, the value of log5 512 is: | |||||||||||||||||||||||||||||||||||||||
Answer: Option C Explanation:
|
| 3. |
|
|||||||||||||||||||||||||||
Answer: Option C Explanation:
|
| 4. | If log 27 = 1.431, then the value of log 9 is: | |||||||
Answer: Option C Explanation:
log 27 = 1.431
|
| 5. |
|
|||||||||||||||||||||||
Answer: Option A Explanation:
So, a + b = 1. |
 log (2 + 3)
log (2 + 3)  log (2 x 3)
log (2 x 3) log 8
log 8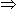 log (33 ) = 1.431
log (33 ) = 1.431